When power sensors are designed, attempts are made to produce the lowest VSWR (SWR) so that the user will have the best match when they use it. However match is never perfect because no device including any power sensor has a perfect SWR. For this reason, two power sensors of equal quality and calibration will read differently in a user’s system. In this brief, we’ll take a look at the reasons for this along with ways to achieve the best power measurements.

As a result of manufacturing limits, part & component variations, line lengths and detector properties, the VSWR of any power sensor is not perfect and varies dramatically over frequency. Two high quality, high performance power sensors will exhibit different VSWR characteristics at different frequencies. Figure 1, a chart from a LadyBug LB5940A Power Sensor data sheet, shows the specifications and typical data for a production run of power sensors. In the data sheet, the company also provides a table with limit (red line in Figure 1) and typical data for several frequency ranges to make uncertainty calculations easier for users. It is also apparent that as the frequency increases, VSWR increases making it very important to understand match when working with higher frequencies.

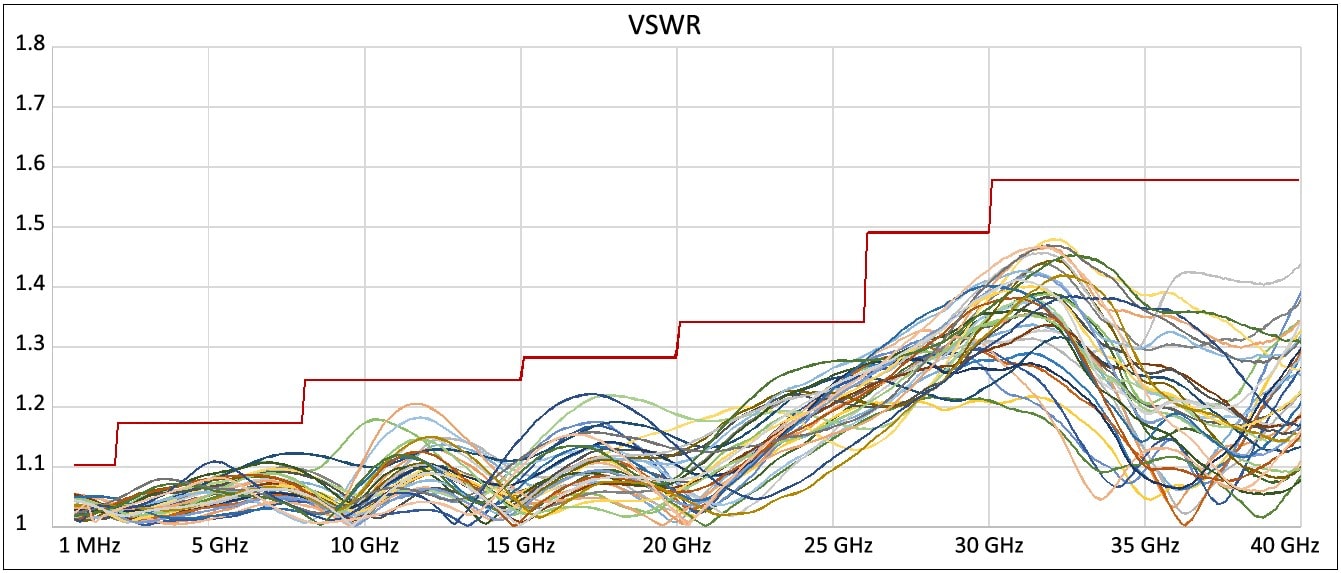
Figure 1 – LB5940A VSWR

Download this Whitepaper: How Match Affects Power Measurements

When comparing first quality power sensors, you might notice that each one could exhibit a better VSWR than the other at some frequencies, even though in total they are similar. For example, at 1 GHz, the LadyBug LB5918A sensor has a limit specification of 1.13 while the Keysight™ U2000 is 1.15; At 15 GHz, both limit specifications are identical. Each one will have a frequency where it has a slightly better match. You can expect an accurate measurement from either of these sensors, however you can be sure that the actual VSWR of each sensor will not be the same. The different VSWR results in different sensor-to-DUT mismatch and slightly different power readings. Further, when phase is considered, power reading variations can exceed 0.1 to 0.2 dB. This sometimes leads to confusion. Next, we will look at it in more detail.

Let’s consider a microwave source set to 1.00 dBm, connected to a power sensor. If the calibration and match of the source and sensor were perfect, you would set and read 1.00 dBm. In reality, sources are calibrated with a 50 ohm load, however the actual output impedance is not 50 ohms. This is due to the source’s broad driver requirements, driver technology limitations and part variations. In fact the VSWR is probably very different than 50 ohms, resulting in a high VSWR. A review of the published VSWR specifications for 4 different current model, top brand sources was 1.5, 1.6, 1.9 and 1.6 at 3 GHz.

Even though a power senor’s typical VSWR is much lower than that of a source, the significant source reflection can result in an error that should be accounted for. This error is a result of a small portion of the power being reflected back from the sensor to the source, a portion of which is then re-reflected by the source and combined into the measurement (See Figure 2). 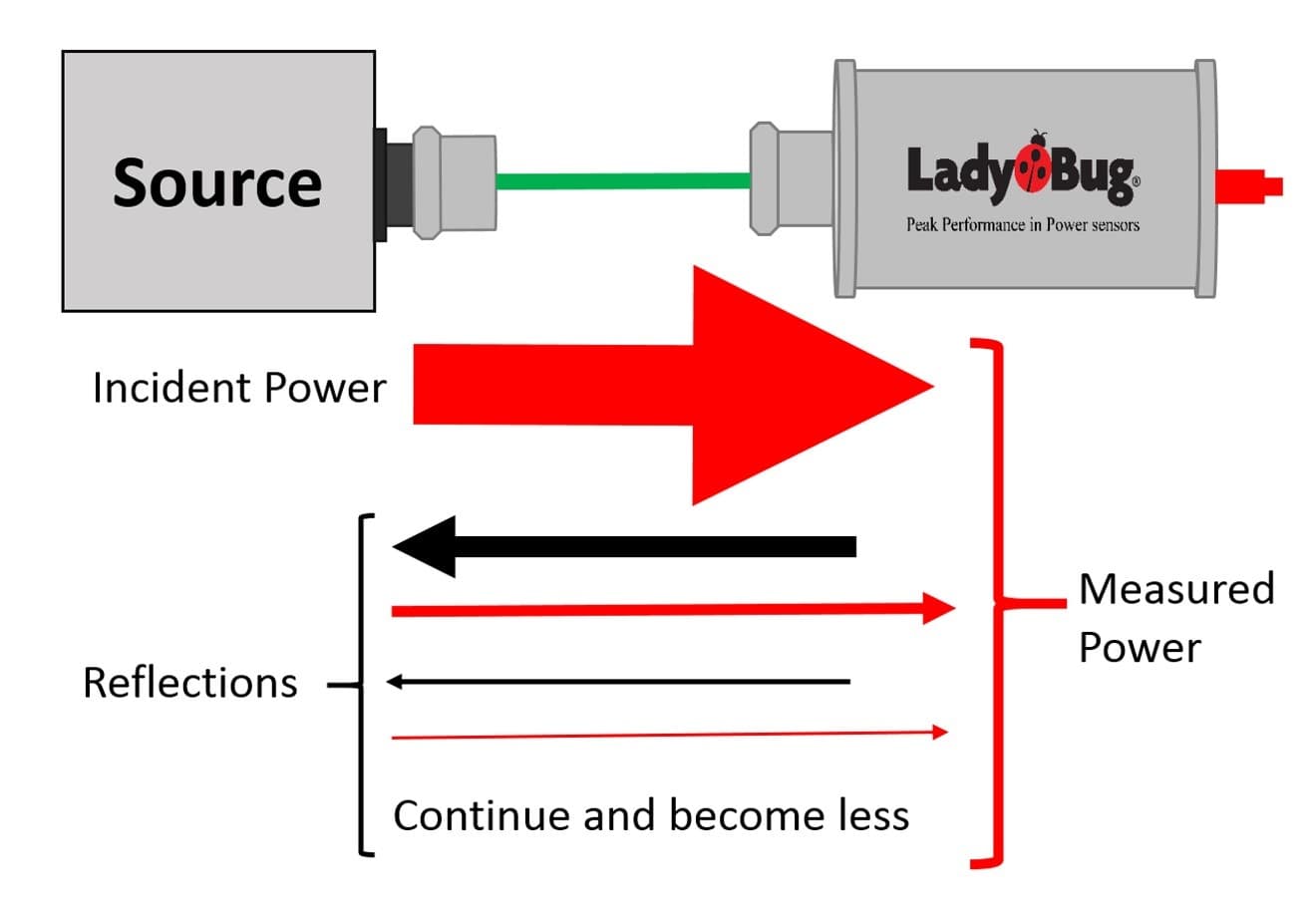In addition to the amplitude, it is important to understand how the reflections’ phase can affect your measurement; if the reflected portion is in phase with the incident power, the measurement will be increased; if the reflected portion is 180 degrees out of phase, the measurement will be reduced; there will be frequencies at which the phase is just right and a perfect result will be produced. The reflection repeats, becoming smaller each time. The total mismatch determines the magnitude of reflected power. In this case it is nice to think of reflection coefficient rather than VSWR even though they are functionally equivalent. The source could be any device generating power for measurement and it is important to know its VSWR.

Figure 2 – Incident & Reflections

To calculate the potential error, you must know the reflection coefficient (ρ) of the sensor and the source (DUT – device under test). The sensor’s ρ can easily be calculated from its specifications. All calculations are done with linear data. We’ll calculate here based on a VSWR of 1.10 to keep things simple. For this example, we will consider these to be limit specifications (worst case numbers).

ρsens = (VSWR-1)/(VSWR+1)

ρsens = (1.10-1)/(1.10+1) = 0.048 = 4.8%

This worst case number indicates that 4.8% of the power could be reflected back. During calibration, match is mitigated in the applied power system so that the sensor can be calibrated correctly. All power is measured, including that which was reflected back.

Now let’s do the same for a source. Here we will use 1.3 VSWR which is something that we might expect to see.

ρDUT = (VSWR-1)/(VSWR+1)

ρDUT = (1.3-1)/(1.3+1) = 0.1304 = 13.04%

If the above described source and sensor are directly connected there will be interaction due to the reflected power. Let’s calculate the mismatch interaction and total potential error due to mismatch using the formula:

Mm = (1+(ρsens * ρDUT))2-1

Mm = (1+(.048*.1304))2-1 = 0.0126 = 1.26%

The potential error in measurement due to mismatch is 1.26%. Since limit values (worst case specifications) were used, the error would be something less than this. If we had located and used typical numbers, we would have had a smaller number that was probably more accurate instead of this worst case result.

If we now consider a different power sensor which has a similar but not exact VSWR we will see slightly different results even if the calibrations are both perfect.

This second sensor has a VSWR of 1.11, just slightly different than the first.

ρsens = (VSWR-1)/(VSWR+1)

ρsens = (1.11-1)/(1.11+1) = 0.052 = 5.2%

The worst case number for the second sensors shows that 5.2% of the power could be reflected back from the sensor.

Since there is no change in the source, we can use ρDUT of 0.1304 and calculate the combined result as:

Mm = (1+(ρsens * ρDUT))2-1

Mm = (1+(0.052*0.1304))2-1 = 0.0136 = 1.36%

The potential error in this measurement due to mismatch is 1.36%, very close to the former 1.26%. However you can not expect both sensors to measure exactly the same even though both are good measurements.

As can be seen, even if you have the very highest level of calibration, match can cause significant measurement uncertainty. Mismatch is generally considered the most significant part of total measurement uncertainty.

In cases where high source mismatch is present, uncertainty can be reduced by adding an attenuator to the system. If, for example, a 3 dB attenuator is inserted between the source and sensor, the returned power from the sensor to the DUT is reduced, then the resultant reflection back from the DUT is again reduced, minimizing the error. Additional reflections are added on each side of the attenuator, however in cases where large source mismatch presents an issue, these attenuator mismatch errors are generally small in comparison to the larger source mismatch. Users requiring the highest level of accuracy should take all factors into account.

While mismatch is usually the most significant component of a measurement’s uncertainty it is only one of many. Another component is the sensors Calibration Factor uncertainty. This important uncertainty represents the accuracy of the sensors calibration, and is often stated by manufacturers as the sensors accuracy because the DUT mismatch is unknown. However sensor-to-DUT mismatch is most often a more significant uncertainty.

An easy way to begin calculating measurement uncertainty and increase your overall measurement accuracy and understanding, is to workup the uncertainty of a measurement using a power sensor manufacturer’s uncertainty worksheet or spreadsheet. For example, the last pages of the above mentioned LB5940A power sensor’s datasheet includes a work sheet and completed example that covers the most significant factors in a typical power sensor measurement. Most high quality power sensor manufacturers provide similar worksheets.

A power sensor manufacturer can supply specifications, however it is not possible to determine the accuracy of any measurement without knowing the measurements parameters. Most of the specifications have an associated parameter such as frequency or power level. These will determine which specification from the sensors data sheet are applicable. Once these are all known, they can be included in an RSS calculation to determine the total measurement uncertainty.

In conclusion, for the best accuracy, make the distinction between sensor accuracy and measurement accuracy, then use the sensor’s specifications to develop a full understanding of your measurement’s uncertainty. This will give you confidence in the measurement and allow you to improve the accuracy as needed.